Дифференциальное исчисление: от основ до применения в современной науке

Производная — это фундаментальное понятие в математике, описывающее скорость изменения функции. Она показывает, насколько быстро меняется значение функции при малом изменении аргумента. Производная играет ключевую роль в дифференциальном исчислении, разработанном Исааком Ньютоном и Готфридом Лейбницем.

Производная необходима для решения множества задач в науке и технике:

• Определение скорости и ускорения в физике
• Оптимизация функций в экономике и инженерии
• Анализ скорости химических реакций
• Исследование роста популяций в биологии
• Расчет траекторий в космонавтике

Физический смысл производной на примерах

Физический смысл производной легко понять на конкретных примерах из реальной жизни:

• Скорость автомобиля — производная пройденного пути по времени
• Ускорение — производная скорости по времени
• Сила тока — производная заряда по времени
• Плотность вещества — производная массы по объему
• Теплопроводность — производная теплового потока по градиенту температуры

В экономике производная также находит применение. Например, предельная прибыль — это производная функции прибыли по объему производства. Она показывает, как изменится прибыль при небольшом увеличении выпуска продукции.

Основные правила дифференцирования

Для вычисления производных существует ряд основных правил:

• Производная константы равна нулю
• Производная суммы равна сумме производных
• Производная произведения: (uv)’ = u’v + uv’
• Производная частного: (u/v)’ = (u’v — uv’) / v²
• Правило цепной функции: (f(g(x)))’ = f'(g(x)) * g'(x)

Эти правила позволяют находить производные сложных функций, разбивая их на более простые составляющие. Институт математики им. В.А. Стеклова РАН рекомендует начинать изучение дифференцирования именно с этих базовых принципов.

Производные элементарных функций

Знание производных элементарных функций — основа дифференциального исчисления. Вот некоторые ключевые формулы:

• (x^n)’ = nx^(n-1)
• (sin x)’ = cos x
• (cos x)’ = -sin x
• (e^x)’ = e^x
• (ln x)’ = 1/x

Эти формулы, подобно таблице умножения, требуют запоминания для эффективной работы с производными. Математический институт им. В.А. Стеклова РАН рекомендует уделить особое внимание их изучению.

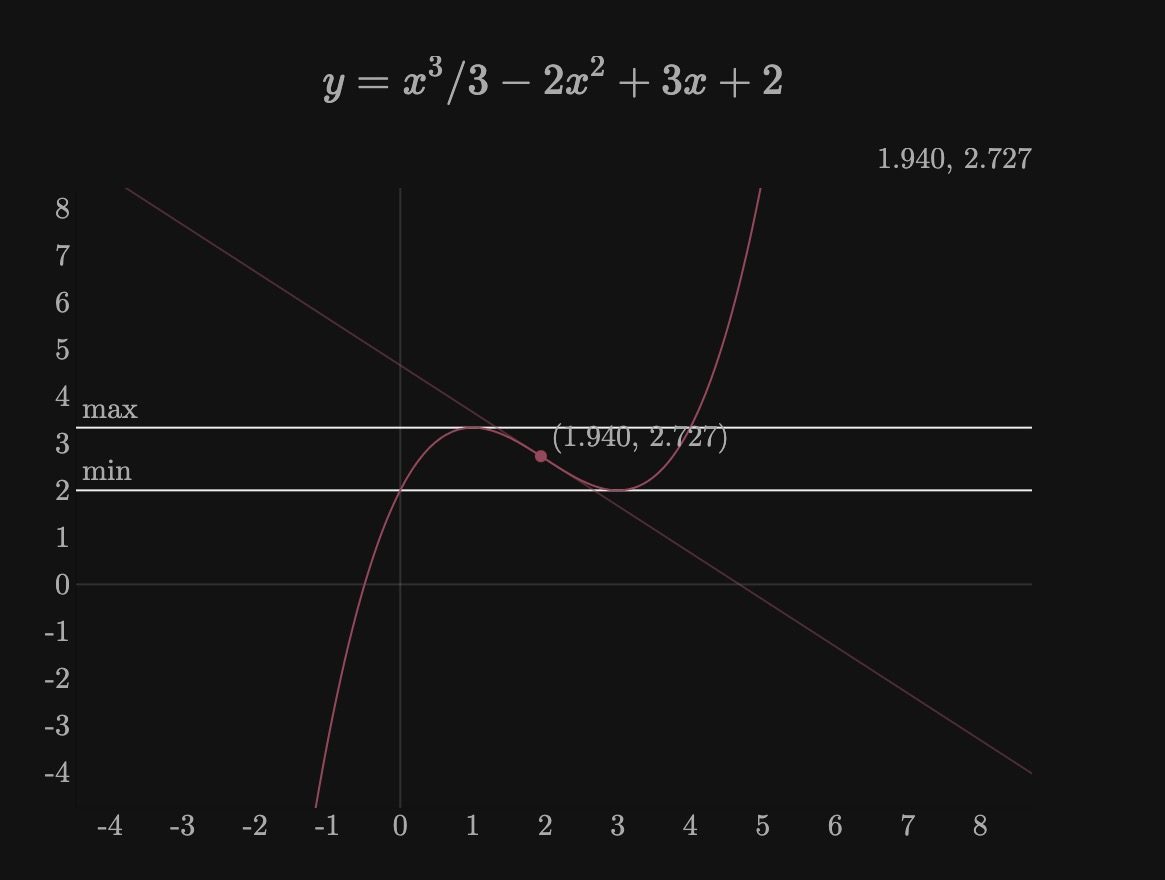
Геометрическая интерпретация производной

Геометрически производная функции в точке представляет собой угловой коэффициент касательной к графику функции в этой точке. Это позволяет визуализировать концепцию производной:

• Положительная производная: функция возрастает
• Отрицательная производная: функция убывает
• Нулевая производная: локальный экстремум или точка перегиба

Эта интерпретация помогает понять поведение функции и находить ее экстремумы, что широко применяется в оптимизационных задачах.

Применение производных в реальной жизни

Производные находят широкое применение в различных областях:

• Физика: расчет скорости и ускорения
• Экономика: анализ предельных издержек и прибыли
• Инженерия: оптимизация конструкций
• Медицина: анализ распространения эпидемий
• Метеорология: прогнозирование погоды

Например, в экономике производная функции спроса по цене показывает, как изменится спрос при небольшом изменении цены. Это помогает компаниям оптимизировать ценовую политику.

В инженерии производные используются для минимизации расхода топлива в двигателях или максимизации прочности конструкций при минимальном весе. Это ключевой инструмент в современном проектировании.

Типичные ошибки при работе с производными

При изучении и применении производных студенты часто допускают следующие ошибки:

• Неправильное применение правила произведения
• Забывание цепного правила для сложных функций
• Ошибки в знаках при дифференцировании тригонометрических функций
• Неверное определение области определения функции
• Пропуск констант при интегрировании

Профессор МГУ им. М.В. Ломоносова отмечает, что многие ошибки связаны с недостаточной практикой и механическим запоминанием формул без понимания их сути.

Как научиться находить производные быстро и легко

Для эффективного освоения техники дифференцирования рекомендуются следующие методы:

• Регулярная практика с разнообразными примерами
• Использование мнемонических правил для запоминания формул
• Визуализация процесса дифференцирования
• Применение компьютерных программ для проверки результатов
• Участие в математических форумах и обсуждениях

Эксперты из Математического института им. В.А. Стеклова РАН подчеркивают важность понимания физического и геометрического смысла производной для более глубокого усвоения материала.

Заключение: ключевые моменты в понимании производных

Подводя итоги, выделим основные аспекты понимания производных:

• Производная — это скорость изменения функции
• Физический смысл производной варьируется в зависимости от контекста
• Основные правила дифференцирования — ключ к решению сложных задач
• Геометрическая интерпретация помогает визуализировать концепцию
• Практическое применение производных охватывает множество областей

Освоение производных открывает широкие возможности в математике, физике, экономике и инженерии. Это фундаментальный инструмент для анализа и оптимизации различных процессов в современном мире.