Геометрия 7-9 класс: формулы площадей, теоремы и практическое применение
Геометрия предлагает ряд формул для вычисления площадей различных фигур. Эти формулы являются основой для решения задач и практических расчетов.
- Треугольник: S = (1/2) * a * h, где a — основание, h — высота
- Прямоугольник: S = a * b, где a и b — стороны
- Квадрат: S = a², где a — сторона
- Параллелограмм: S = a * h, где a — сторона, h — высота
- Ромб: S = (d1 * d2) / 2, где d1 и d2 — диагонали
- Трапеция: S = (a + b) * h / 2, где a и b — основания, h — высота
- Круг: S = πr², где r — радиус
Институт математики и механики УрО РАН рекомендует использовать эти формулы как базовые для решения геометрических задач.
Как решать задачи на площадь треугольника
Решение задач на площадь треугольника требует знания нескольких ключевых формул и методов. Основная формула — S = (1/2) * a * h, где a — основание, h — высота.
Для прямоугольного треугольника можно использовать формулу S = (1/2) * a * b, где a и b — катеты. Формула Герона применяется, когда известны все стороны треугольника: S = √(p(p-a)(p-b)(p-c)), где p — полупериметр.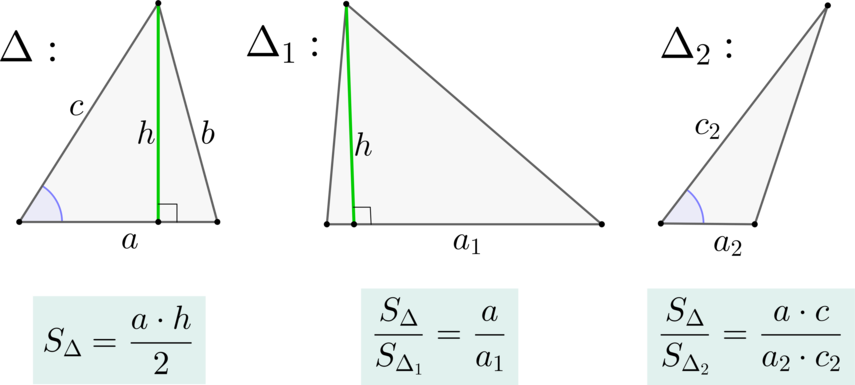
При решении задач важно:
- Определить тип треугольника (прямоугольный, равносторонний, произвольный)
- Выбрать подходящую формулу
- Правильно подставить известные величины
- Выполнить вычисления, соблюдая единицы измерения
Вычисление площади четырехугольников: прямоугольник, квадрат, ромб
Вычисление площади четырехугольников основывается на специфических формулах для каждого типа фигуры.
| Фигура | Формула | Примечание |
|---|---|---|
| Прямоугольник | S = a * b | a и b — стороны |
| Квадрат | S = a² | a — сторона |
| Ромб | S = (d1 * d2) / 2 | d1 и d2 — диагонали |
Для прямоугольника и квадрата формулы просты и интуитивно понятны. Ромб требует знания длин диагоналей. При решении задач на площадь четырехугольников важно правильно идентифицировать фигуру и использовать соответствующую формулу.
Площадь круга и его частей: формулы и примеры
Формула площади круга: S = πr², где r — радиус. Для частей круга используются следующие формулы:
- Сектор: S = (πr² * α) / 360°, где α — центральный угол в градусах
- Сегмент: S = (πr² * α) / 360° — (1/2)r² * sin α, где α — центральный угол в радианах
- Кольцо: S = π(R² — r²), где R — внешний радиус, r — внутренний радиус
Пример: Найти площадь круга с радиусом 5 см. Решение: S = π * 5² ≈ 78,54 см².
При работе с частями круга важно помнить о переводе градусов в радианы и наоборот.
Комбинированные фигуры: методы расчета площади
Расчет площади комбинированных фигур требует декомпозиции на простые элементы. Основные методы:
- Разбиение на простые фигуры и суммирование их площадей
- Вычитание площади одной фигуры из другой
- Использование координатной плоскости для сложных форм
Пример: Площадь фигуры, состоящей из прямоугольника и полукруга, равна сумме их площадей. При решении таких задач может потребоваться знание квадратных уравнений.
Практическое применение формул площади в реальной жизни
Формулы площади широко применяются в различных сферах:
- Строительство: расчет материалов для отделки помещений
- Ландшафтный дизайн: планирование газонов и клумб
- Архитектура: проектирование зданий и сооружений
- Сельское хозяйство: определение площади посевных участков
- Картография: измерение площади географических объектов
Пример: Для покраски стен комнаты размером 5×4 м и высотой 2,5 м нужно рассчитать площадь стен: S = 2(5+4) * 2,5 = 45 м².
Типичные ошибки при решении задач на площадь
При решении задач на площадь часто встречаются следующие ошибки:
- Неправильный выбор формулы для конкретной фигуры
- Путаница между периметром и площадью
- Ошибки в единицах измерения (см² вместо м² и т.д.)
- Неверное определение высоты в треугольниках и трапециях
- Забывание о делении на 2 в формулах для треугольника и трапеции
- Некорректное округление результатов
Чтобы избежать этих ошибок, важно внимательно читать условие задачи, проверять выбор формулы и следить за единицами измерения.
FAQ: часто задаваемые вопросы о площадях фигур
Вот ответы на часто задаваемые вопросы о площадях фигур:
Как найти площадь неправильного многоугольника?
Разбейте его на простые фигуры и суммируйте их площади.
Влияет ли поворот фигуры на ее площадь?
Нет, площадь фигуры не зависит от ее положения.
Как связаны площадь и периметр?
Прямой зависимости нет. Фигуры с одинаковым периметром могут иметь разную площадь.
Можно ли найти площадь треугольника, зная только стороны?
Да, используя формулу Герона.
Эти вопросы часто встречаются при изучении геометрии в школе и при решении практических задач.
Заключение: ключевые моменты в расчетах площадей
Подводя итоги, отметим ключевые моменты в расчетах площадей:
- Знание базовых формул для различных геометрических фигур критично
- Важно правильно идентифицировать фигуру и выбрать соответствующую формулу
- При работе с составными фигурами используйте метод декомпозиции
- Всегда проверяйте единицы измерения и правильность вычислений
- Практикуйтесь в решении разнообразных задач для развития навыков
Помните, что умение рассчитывать площади имеет широкое практическое применение в различных областях, от строительства до дизайна.