Квадратные уравнения: формулы, методы и примеры решения

Квадратное уравнение — это алгебраическое уравнение второй степени вида ax^2 + bx + c = 0, где a, b, c — числовые коэффициенты, а x — неизвестная. Коэффициент a не равен нулю, иначе уравнение становится линейным.

Существует три основных вида квадратных уравнений:

• Полное: ax^2 + bx + c = 0 (все коэффициенты не равны нулю)
• Неполное: ax^2 + bx = 0 или ax^2 + c = 0 (один из коэффициентов равен нулю)
• Приведенное: x^2 + px + q = 0 (коэффициент a равен 1)

Решение квадратного уравнения заключается в нахождении значений x, при которых уравнение обращается в верное числовое равенство. Эти значения называются корнями уравнения.

Формула дискриминанта: ключ к решению

Дискриминант — ключевое понятие в теории квадратных уравнений. Он определяет количество и характер корней уравнения. Формула дискриминанта: D = b^2 — 4ac, где a, b, c — коэффициенты квадратного уравнения.

Интерпретация значений дискриминанта:

• D > 0: уравнение имеет два различных действительных корня
• D = 0: уравнение имеет один действительный корень (двойной корень)
• D < 0: уравнение не имеет действительных корней

Дискриминант используется в формуле корней квадратного уравнения и позволяет быстро определить природу решений без полного вычисления корней.

Алгоритм решения полного квадратного уравнения

Для решения полного квадратного уравнения ax^2 + bx + c = 0 используется следующий алгоритм:

1. Вычислить дискриминант: D = b^2 — 4ac
2. Определить количество корней по значению дискриминанта
3. Вычислить корни по формуле: x1,2 = (-b ± √D) / (2a)
4. Записать ответ в зависимости от значения дискриминанта

Пример решения: для уравнения x^2 — 5x + 6 = 0

• a = 1, b = -5, c = 6
• D = (-5)^2 — 4*1*6 = 25 — 24 = 1
• x1 = (5 + √1) / (2*1) = 3
• x2 = (5 — √1) / (2*1) = 2

Ответ: x1 = 3, x2 = 2. Проверка: 3^2 — 5*3 + 6 = 0 и 2^2 — 5*2 + 6 = 0.

Особенности решения неполных квадратных уравнений

Неполные квадратные уравнения имеют упрощенный вид и решаются особыми методами:

1. ax^2 + bx = 0 (c = 0):
   • Вынести за скобки общий множитель x: x(ax + b) = 0
   • Решить уравнение: x = 0 или ax + b = 0
   • Второй корень: x = -b/a
2. ax^2 + c = 0 (b = 0):
   • Выразить x^2: x^2 = -c/a
   • Извлечь квадратный корень: x = ±√(-c/a)
   • Решение существует только при -c/a ≥ 0

Пример: 3x^2 — 12 = 0
x^2 = 4
x = ±2
Ответ: x1 = 2, x2 = -2

Графический метод решения квадратных уравнений

Графический метод основан на построении параболы y = ax^2 + bx + c и нахождении точек ее пересечения с осью x.

Алгоритм решения:

1. Построить график функции y = ax^2 + bx + c
2. Найти точки пересечения графика с осью x
3. Определить x-координаты этих точек — они являются корнями уравнения

Интерпретация результатов:

• Две точки пересечения: два различных корня
• Одна точка касания: один двойной корень
• Нет пересечений: действительных корней нет

Графический метод наглядно демонстрирует связь между уравнением и его геометрическим представлением, что полезно для понимания природы решений.

Теорема Виета: связь между корнями и коэффициентами

Теорема Виета устанавливает связь между корнями квадратного уравнения и его коэффициентами. Для уравнения ax^2 + bx + c = 0 с корнями x1 и x2:

• x1 + x2 = -b/a (сумма корней)
• x1 * x2 = c/a (произведение корней)

Применение теоремы Виета:

1. Проверка правильности найденных корней
2. Составление квадратного уравнения по известным корням
3. Нахождение одного корня, если известен другой

Пример: для уравнения x^2 — 5x + 6 = 0
Корни: x1 = 3, x2 = 2
Проверка: 3 + 2 = 5 (-b/a) и 3 * 2 = 6 (c/a)

Теорема Виета значительно упрощает работу с квадратными уравнениями и позволяет быстро анализировать свойства их решений.

Проверка корней квадратного уравнения

Проверка корней — важный этап решения квадратного уравнения. Она позволяет убедиться в правильности полученных результатов. Существует несколько методов проверки:

1. Подстановка корней в исходное уравнение:
   • Подставить каждый найденный корень в уравнение ax^2 + bx + c = 0
   • Вычислить значение левой части уравнения
   • Если результат равен нулю, корень верный
2. Использование теоремы Виета:
   • Проверить, удовлетворяют ли найденные корни соотношениям x1 + x2 = -b/a и x1 * x2 = c/a
3. Графический метод:
   • Построить график функции y = ax^2 + bx + c
   • Убедиться, что найденные корни соответствуют точкам пересечения графика с осью x

Пример проверки: Для уравнения x^2 — 5x + 6 = 0 найдены корни x1 = 3, x2 = 2.
Подстановка: 3^2 — 5*3 + 6 = 9 — 15 + 6 = 0 и 2^2 — 5*2 + 6 = 4 — 10 + 6 = 0.
Корни верны.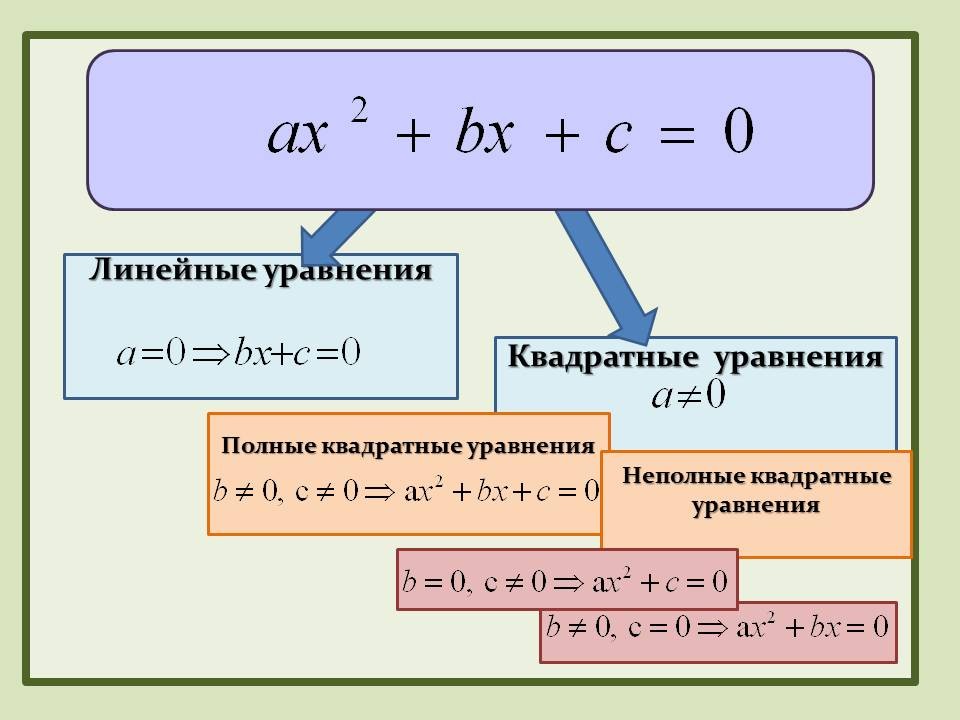

Типичные ошибки при решении квадратных уравнений

При решении квадратных уравнений часто допускаются следующие ошибки:

• Неправильное определение коэффициентов a, b, c
• Ошибки в вычислении дискриминанта
• Неверное использование знаков «+» и «-» в формуле корней
• Деление на ноль при a = 0
• Пропуск второго корня при решении неполных уравнений
• Ошибки в арифметических вычислениях
• Неправильное округление результатов
• Забывание проверки найденных корней

Рекомендации по избежанию ошибок:

1. Внимательно записывать уравнение в стандартной форме ax^2 + bx + c = 0
2. Использовать калькулятор для сложных вычислений
3. Всегда проверять найденные корни
4. Практиковаться на различных типах квадратных уравнений
5. Использовать альтернативные методы решения для проверки результатов

Понимание этих типичных ошибок и методов их предотвращения поможет повысить точность и эффективность решения квадратных уравнений.