
Теория вероятностей и статистика: от фундаментальных основ до практического применения
Вероятность и статистика — это разделы математики, изучающие случайные события и анализ данных. Вероятность оценивает шансы наступления событий. Статистика собирает, анализирует и интерпретирует данные.
Вероятность помогает предсказывать будущие события на основе известной информации. Статистика позволяет делать выводы о больших группах, изучая их части. Вместе они формируют мощный инструментарий для принятия решений в условиях неопределенности.
Основные понятия теории вероятностей
Теория вероятностей оперирует следующими ключевыми понятиями:
- Событие — результат эксперимента
- Вероятность — число от 0 до 1, характеризующее возможность наступления события
- Случайная величина — величина, принимающая различные значения с определенными вероятностями
- Распределение вероятностей — закон, описывающий вероятности всех возможных значений случайной величины
Фундаментальные аксиомы теории вероятностей были сформулированы Андреем Колмогоровым в 1933 году. Они лежат в основе современного математического подхода к изучению случайности.
Ключевые концепции статистики для начинающих
Статистика использует следующие базовые концепции:
- Выборка — подмножество объектов из изучаемой совокупности
- Среднее значение — мера центральной тенденции данных
- Медиана — значение, делящее выборку на две равные части
- Мода — наиболее часто встречающееся значение
- Дисперсия — мера разброса данных
- Стандартное отклонение — квадратный корень из дисперсии
Американская статистическая ассоциация (ASA) рекомендует использовать эти концепции для базового анализа данных. Программа R, разработанная R Foundation for Statistical Computing, широко применяется для статистических вычислений.
Методы расчета вероятности событий
Существует несколько основных методов расчета вероятности:
- Классический метод: отношение числа благоприятных исходов к общему числу исходов
- Статистический метод: частота появления события в серии экспериментов
- Геометрический метод: отношение мер геометрических фигур
- Аксиоматический метод: вычисление на основе аксиом теории вероятностей
Формула полной вероятности и теорема Байеса позволяют решать более сложные задачи. Для олимпиадных задач часто требуются продвинутые методы.
Статистические распределения и их применение
Ключевые статистические распределения включают:
- Нормальное распределение: описывает многие природные явления
- Биномиальное распределение: моделирует количество успехов в серии испытаний
- Распределение Пуассона: описывает редкие события
- Экспоненциальное распределение: моделирует время между событиями
Институт инженеров электротехники и электроники (IEEE) использует эти распределения для анализа надежности электронных систем. Фармацевтические компании применяют их при клинических испытаниях лекарств.
Анализ данных: от сбора до интерпретации
Процесс анализа данных включает следующие этапы:
- Сбор данных: опросы, эксперименты, наблюдения
- Очистка данных: удаление ошибок и выбросов
- Исследовательский анализ: визуализация, описательная статистика
- Статистические тесты: проверка гипотез, ANOVA, регрессия
- Интерпретация результатов: выводы, рекомендации
Компания SAS Institute предоставляет программное обеспечение для всех этапов анализа данных. Национальный центр статистики образования США (NCES) использует эти методы для анализа образовательных данных.
Практическое применение вероятности и статистики
Вероятность и статистика широко применяются в различных областях:
- Финансы: оценка рисков, прогнозирование рынков
- Медицина: клинические испытания, эпидемиология
- Страхование: расчет страховых премий
- Маркетинг: анализ потребительского поведения
- Производство: контроль качества продукции
Компания Google использует статистические методы для улучшения поисковых алгоритмов. Центр по контролю и профилактике заболеваний США (CDC) применяет вероятностные модели для прогнозирования эпидемий.
Типичные ошибки при работе с вероятностью и статистикой
Часто встречающиеся ошибки включают:
- Игнорирование размера выборки
- Путаница между корреляцией и причинно-следственной связью
- Неправильная интерпретация p-значений
- Ошибка выжившего
- Пренебрежение эффектом регрессии к среднему
Американская статистическая ассоциация (ASA) выпустила руководство по правильной интерпретации статистических результатов. Журнал Nature регулярно публикует статьи о распространенных статистических заблуждениях в научных исследованиях.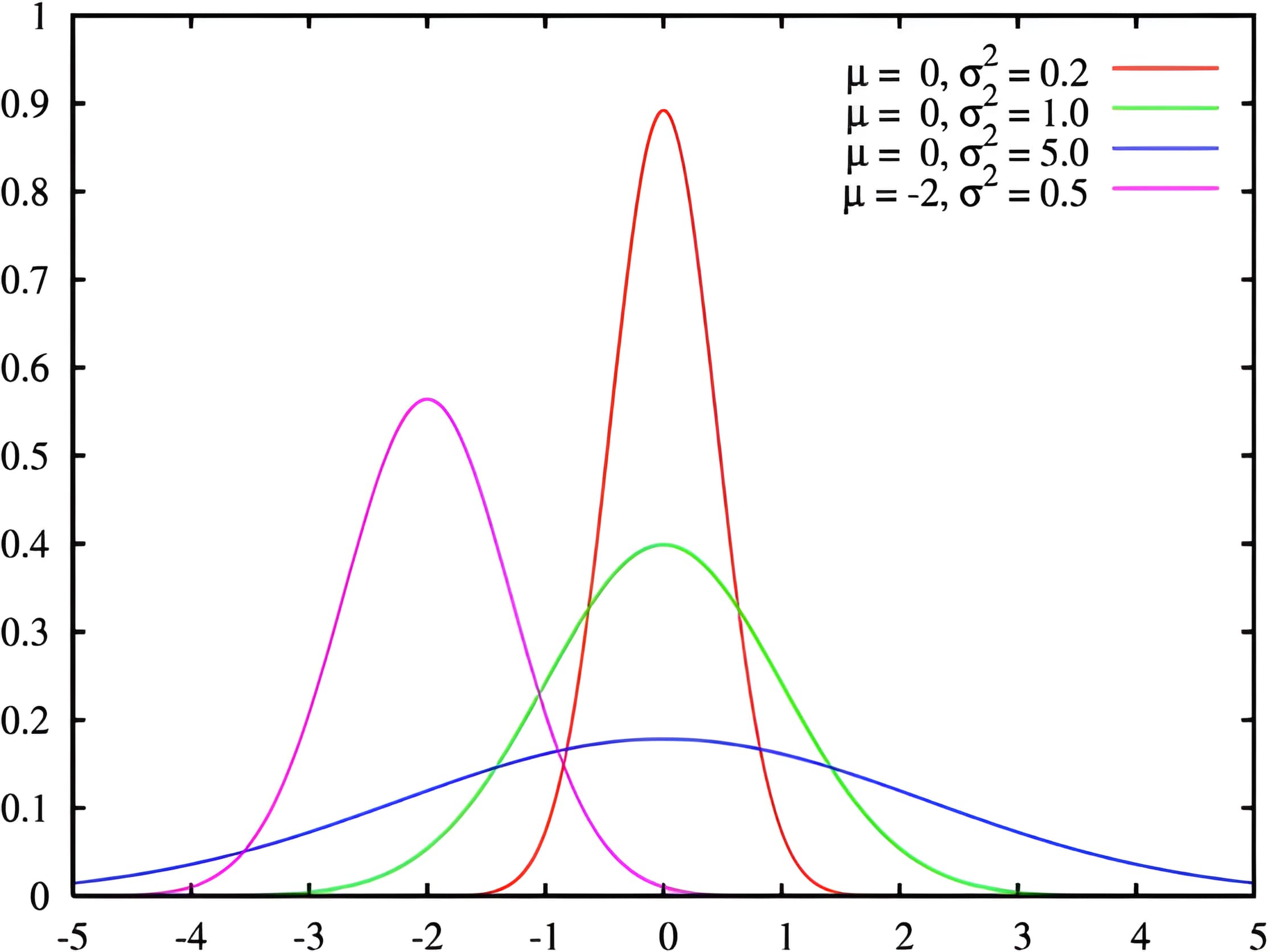
Инструменты и ресурсы для изучения вероятности и статистики
Для изучения вероятности и статистики доступны различные инструменты и ресурсы:
- Программное обеспечение: R, Python (библиотеки NumPy, SciPy, Pandas), SPSS
- Онлайн-курсы: Coursera, edX, Khan Academy
- Учебники: «Основы статистики» Ларри Гонника, «Голая статистика» Чарльза Уилана
- Веб-ресурсы: StatTrek, Math is Fun, Probability Distributions Calculator
Массачусетский технологический институт (MIT) предоставляет бесплатные онлайн-курсы по вероятности и статистике. Национальный институт стандартов и технологий (NIST) поддерживает обширную базу данных статистических методов и ресурсов.




