Тригонометрия: от основ до практического применения
Тригонометрия — раздел математики, изучающий соотношения между сторонами и углами треугольников. Она тесно связана с геометрией и алгеброй. Основные понятия включают угол, радиан и градус.
- Угол: фигура, образованная двумя лучами с общим началом
- Радиан: единица измерения углов, равная углу, опирающемуся на дугу, длина которой равна радиусу
- Градус: альтернативная единица измерения углов, где полный оборот равен 360°
Тригонометрия находит широкое применение в физике, инженерии и астрономии. Она используется для расчетов в навигации, архитектуре и электротехнике.
Тригонометрические функции: синус, косинус, тангенс
Основные тригонометрические функции — синус (sin), косинус (cos) и тангенс (tan). Они описывают отношения сторон прямоугольного треугольника.
- Синус: отношение противолежащего катета к гипотенузе
- Косинус: отношение прилежащего катета к гипотенузе
- Тангенс: отношение противолежащего катета к прилежащему
Дополнительные функции включают котангенс (cot), секанс (sec) и косеканс (csc). Все эти функции периодичны и имеют характерные графики.
Тригонометрический круг и его применение
Тригонометрический круг — это единичная окружность на координатной плоскости. Он помогает визуализировать тригонометрические функции и их значения.
- Радиус круга равен 1
- Центр круга находится в начале координат (0,0)
- Точка на окружности определяется углом поворота от оси x
Круг разделен на четыре четверти, каждая соответствует диапазону значений функций. Используя тригонометрический круг, можно легко определить знаки и значения функций для любого угла.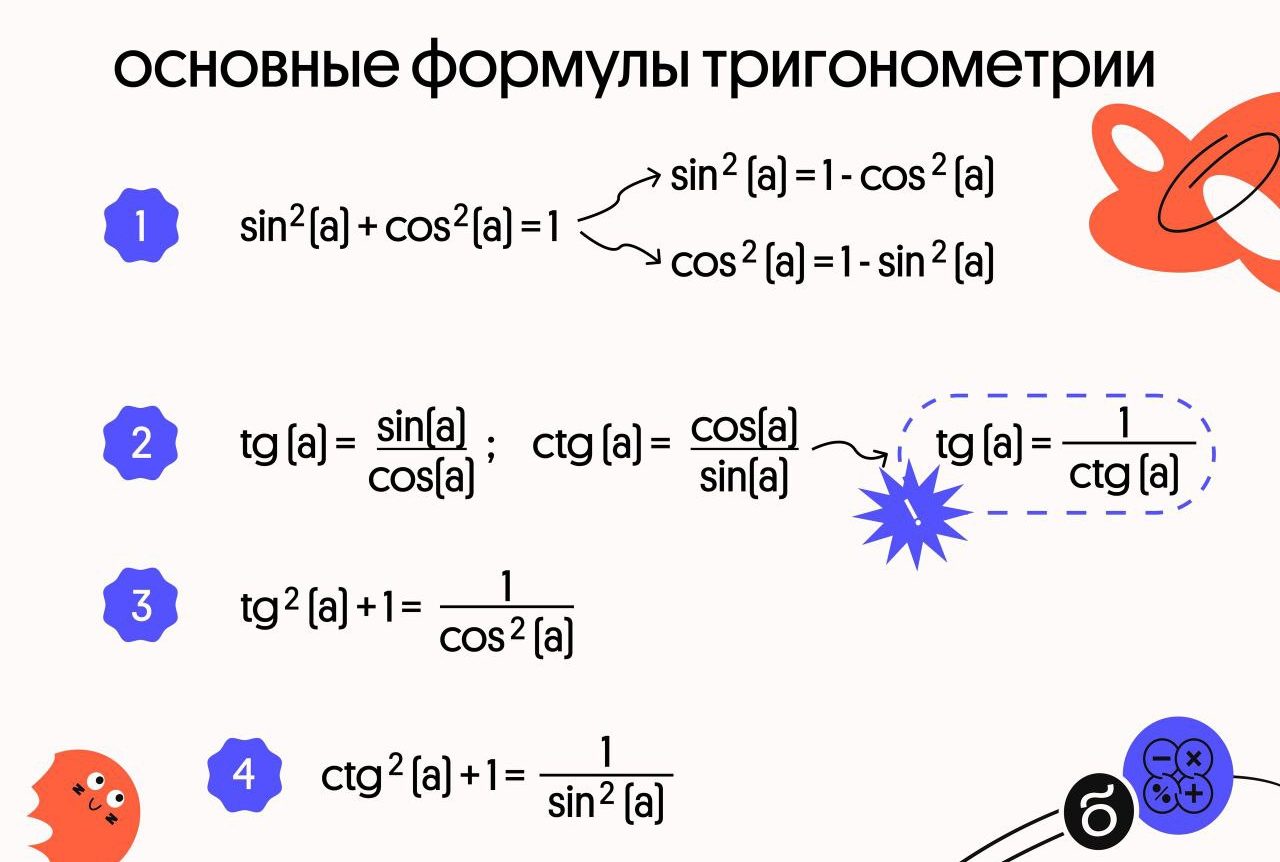
Основные тригонометрические формулы
Тригонометрические формулы — ключевой инструмент для решения задач. Они позволяют преобразовывать и упрощать выражения.
- Формулы сложения: sin(α+β) = sinα cosβ + cosα sinβ
- Формулы двойного угла: cos2α = cos²α — sin²α
- Формулы половинного угла: sin(α/2) = ±√((1-cosα)/2)
Важно помнить основное тригонометрическое тождество: sin²α + cos²α = 1. Оно применяется во многих вычислениях и доказательствах.
Решение треугольников в тригонометрии
Решение треугольников — это нахождение неизвестных элементов треугольника по известным. Основные инструменты:
- Теорема синусов: a/sinA = b/sinB = c/sinC
- Теорема косинусов: c² = a² + b² — 2ab cosC
- Формулы для площади треугольника
Эти методы применяются в геодезии, навигации и строительстве. Они также связаны с финансовыми расчетами.
Практическое применение тригонометрии в реальной жизни
Тригонометрия широко используется в различных областях:
- Архитектура: расчет углов наклона крыш, высоты зданий
- Навигация: определение курса судов и самолетов
- Астрономия: измерение расстояний до небесных тел
- Физика: анализ колебаний и волн
- Электротехника: работа с переменным током
NASA применяет тригонометрию для расчета траекторий космических аппаратов. В медицине она используется в томографии и ультразвуковой диагностике.
Типичные ошибки начинающих при изучении тригонометрии
При изучении тригонометрии новички часто сталкиваются с рядом трудностей. Вот наиболее распространенные ошибки:
- Путаница в знаках функций в разных четвертях
- Неправильное использование единиц измерения углов (градусы вместо радиан)
- Ошибки при работе с обратными тригонометрическими функциями
- Непонимание периодичности функций
- Сложности с применением формул приведения
Профессор Массачусетского технологического института Гилберт Стрэнг отмечает: «Ключ к пониманию тригонометрии — это практика и визуализация концепций».
Заключение: ключевые моменты для успешного освоения тригонометрии
Для эффективного изучения тригонометрии важно:
- Освоить основные понятия и функции
- Регулярно практиковаться в решении задач
- Использовать тригонометрический круг для визуализации
- Понимать связь тригонометрии с геометрией и алгеброй
- Изучать практические применения в реальной жизни
Тригонометрия — мощный инструмент в математике и науке. Её понимание открывает двери к решению сложных задач в физике, инженерии и других областях.